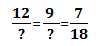Le théorème de Thalès est un théorème géométrique de proportionnalité que l'on utilise avec des triangles: si une droite parallèle à la 'un des côtés du triangle sectionne les deux autres côtés cela forme alors un deuxième triangle semblable.
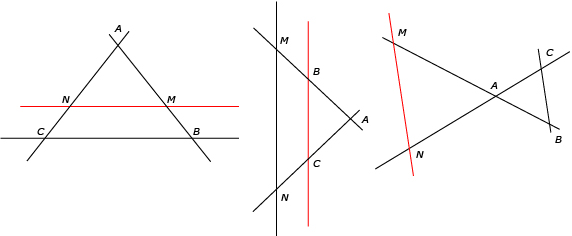
On peut dénombrer trois cas:
Ce théorème permet de calculer des longueurs dans un triangle de et de prouver le parallélisme de deux droites.
Exemple: 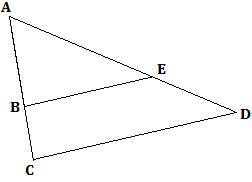
Ici, la droite passant par les points B et est parallèle à la droite passant par les points C et D. D'après le théorème de Thalès, on a:
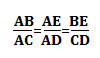
Attention à l'ordre ! Les côtés de "petit triangle" doivent être du même côté par rapport à la barre de fraction.
Pour calculer des longueurs on fait un produit en croix.
Si AB = 12 cm; AE = 9 cm; BE = 7 cm et CD = 18 cm. Que vaut AD?
On a donc -->
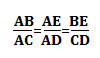
--> on remplace par les valeurs -->
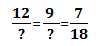
AD = (CD x AE)/ BE --> (18 x 9)/7 = 23,14 cm.
Exemple 2 : Pour prouver que deux droites sont parallèles, il faut par hypothèse partir du fait que les points sont alignés dans le même ordre. On calcule ensuite les rapports et si ceux-ci sont égaux, les droites sont parallèles.
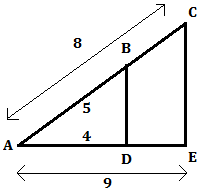
(BD) et (CE) sont-elles parallèles?
On admet que A, B et C et A, D et E sont alignés et dans le même ordre. On a donc les rapports suivants:
AD/AE et AB/AC --> 4/9 et 5/8 --> 0.44 et 0.625. Ici les résutats sont différents donc les droites ne
sont pas parallèles. 
 visites
visites
 visites
visites

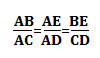 Attention à l'ordre ! Les côtés de "petit triangle" doivent être du même côté par rapport à la barre de fraction.
Attention à l'ordre ! Les côtés de "petit triangle" doivent être du même côté par rapport à la barre de fraction.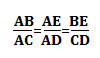 --> on remplace par les valeurs -->
--> on remplace par les valeurs -->